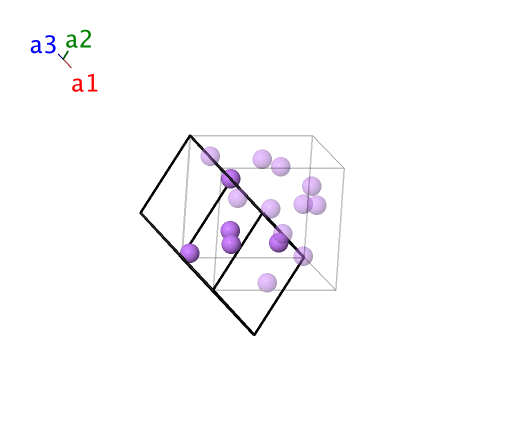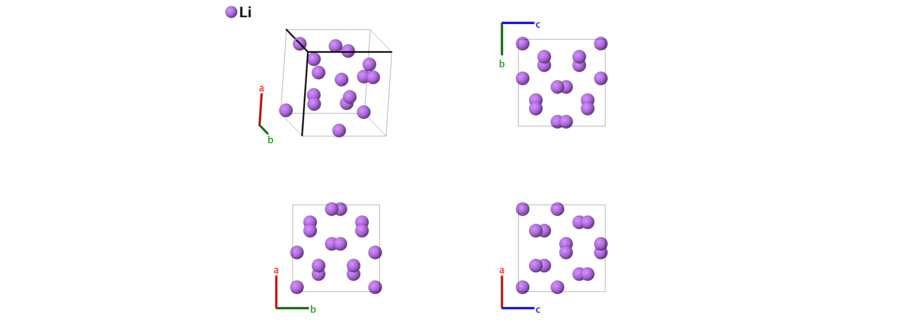
High–pressure cI16 Li Structure: A_cI16_220_c
| Prototype | : | Li |
| AFLOW prototype label | : | A_cI16_220_c |
| Strukturbericht designation | : | None |
| Pearson symbol | : | cI16 |
| Space group number | : | 220 |
| Space group symbol | : | $\text{I}\bar{4}\text{3d}$ |
| AFLOW prototype command | : | aflow --proto=A_cI16_220_c --params=$a$,$x_{1}$ |
Other compounds with this structure
- Na (under pressure)
- This is a high-pressure phase of lithium. We use the data from (Hanfland, 2000) at 38.9 GPa. When $x_{1}$ = 0 this becomes a body-centered cubic (A2) system. We have used the fact that all vectors of the form $( \pm a/2 \mathbf{\hat{x}} \pm a/2 \mathbf{\hat{y}} \pm a/2 \mathbf{\hat{z}} )$ are primitive vectors of the body-centered cubic lattice to simplify the positions of some atoms in both lattice and Cartesian coordinates.
Body-centered Cubic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & - \frac12 \, a \, \mathbf{\hat{x}} + \frac12 \, a \, \mathbf{\hat{y}} + \frac12 \, a \, \mathbf{\hat{z}} \\
\mathbf{a}_2 & = & ~ \frac12 \, a \, \mathbf{\hat{x}} - \frac12 \, a \, \mathbf{\hat{y}} + \frac12 \, a \, \mathbf{\hat{z}} \\
\mathbf{a}_3 & = & ~ \frac12 \, a \, \mathbf{\hat{x}} + \frac12 \, a \, \mathbf{\hat{y}} - \frac12 \, a \, \mathbf{\hat{z}} \\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \text{Lattice Coordinates} & & \text{Cartesian Coordinates} &\text{Wyckoff Position} & \text{Atom Type} \\ \mathbf{B}_{1} & = &2 x_{1} \, \mathbf{a}_{1}+ 2 x_{1} \, \mathbf{a}_{2}+ 2 x_{1} \, \mathbf{a}_{3}& = &x_{1} \, a \, \mathbf{\hat{x}}+ x_{1} \, a \, \mathbf{\hat{y}}+ x_{1} \, a \, \mathbf{\hat{z}}& \left(16c\right) & \text{Li} \\ \mathbf{B}_{2} & = &\frac12 \, \mathbf{a}_{1}+ \left(\frac12 - 2 x_{1}\right) \, \mathbf{a}_{3}& = &- x_{1} \, a \, \mathbf{\hat{x}}+ \left(\frac12 - x_{1}\right) \, a \, \mathbf{\hat{y}}+ x_{1} \, a \, \mathbf{\hat{z}}& \left(16c\right) & \text{Li} \\ \mathbf{B}_{3} & = &\left(\frac12 - 2 x_{1}\right) \, \mathbf{a}_{2}+ \frac12 \, \mathbf{a}_{3}& = &\left(\frac12 - x_{1}\right) \, a \, \mathbf{\hat{x}}+ x_{1} \, a \, \mathbf{\hat{y}}- x_{1} \, a \, \mathbf{\hat{z}}& \left(16c\right) & \text{Li} \\ \mathbf{B}_{4} & = &\left(\frac12 - 2 x_{1}\right) \, \mathbf{a}_{1}+ \frac12 \, \mathbf{a}_{2}& = &+ x_{1} \, a \, \mathbf{\hat{x}}- x_{1} \, a \, \mathbf{\hat{y}}\left(\frac12 - x_{1}\right) \, a \, \mathbf{\hat{z}}& \left(16c\right) & \text{Li} \\ \mathbf{B}_{5} & = &\left(\frac12 + 2 x_{1}\right) \, \mathbf{a}_{1}+ \left(\frac12 + 2 x_{1}\right) \, \mathbf{a}_{2}+ \left(\frac12 + 2 x_{1}\right) \, \mathbf{a}_{3}& = &\left(\frac14 + x_{1}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac14 + x_{1}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac14 + x_{1}\right) \, a \, \mathbf{\hat{z}}& \left(16c\right) & \text{Li} \\ \mathbf{B}_{6} & = &\frac12 \, \mathbf{a}_{1}- 2 x_{1} \, \mathbf{a}_{3}& = &\left(\frac34 - x_{1}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac14 - x_{1}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac14 + x_{1}\right) \, a \, \mathbf{\hat{z}}& \left(16c\right) & \text{Li} \\ \mathbf{B}_{7} & = &- 2 x_{1} \, \mathbf{a}_{1}+ \frac12 \, \mathbf{a}_{2}& = &\left(\frac14 + x_{1}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac34 - x_{1}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac14 - x_{1}\right) \, a \, \mathbf{\hat{z}}& \left(16c\right) & \text{Li} \\ \mathbf{B}_{8} & = &- 2 x_{1} \, \mathbf{a}_{2}+ \frac12 \, \mathbf{a}_{3}& = &\left(\frac14 - x_{1}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac14 + x_{1}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac34 - x_{1}\right) \, a \, \mathbf{\hat{z}}& \left(16c\right) & \text{Li} \\ \end{array} \]References
- M. Hanfland, K. Syassen, N. E. Christensen, and D. L. Novikov, New high–pressure phases of lithium, Nature 408, 174–178 (2000), doi:10.1038/35041515.