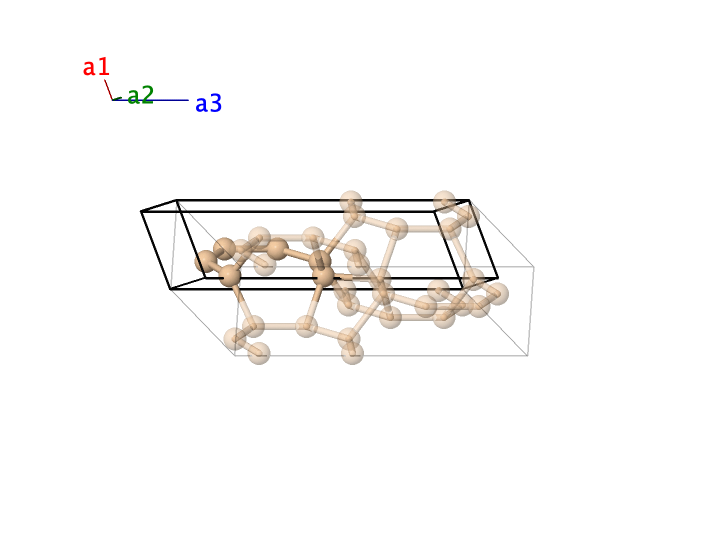
Si24 Clathrate Structure : A_oC24_63_3f
| Prototype | : | Si24 |
| AFLOW prototype label | : | A_oC24_63_3f |
| Strukturbericht designation | : | None |
| Pearson symbol | : | oC24 |
| Space group number | : | 63 |
| Space group symbol | : | $Cmcm$ |
| AFLOW prototype command | : | aflow --proto=A_oC24_63_3f --params=$a$,$b/a$,$c/a$,$y_{1}$,$z_{1}$,$y_{2}$,$z_{2}$,$y_{3}$,$z_{3}$ |
- Unlike the Si34 and Si46 clathrates, this is an experimentally determined structure, prepared by removing sodium atoms from an Na4Si24 predecessor.
- There is no consistency in the naming of these clathrate structures. Si34 and Si46 were named by their authors based on the size of the primitive unit cell. Here, (Kim, 2015) has chosen to name the structure based on the size of the conventional cell. For now, at least, we will follow the authors' naming schemes for these structures.
Base-centered Orthorhombic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & \frac12 \, a \, \mathbf{\hat{x}} - \frac12 \, b \, \mathbf{\hat{y}} \\
\mathbf{a}_2 & = & \frac12 \, a \, \mathbf{\hat{x}} + \frac12 \, b \, \mathbf{\hat{y}} \\
\mathbf{a}_3 & = & c \, \mathbf{\hat{z}} \\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \text{Lattice Coordinates} & & \text{Cartesian Coordinates} &\text{Wyckoff Position} & \text{Atom Type} \\ \mathbf{B}_{1} & = & -y_{1} \, \mathbf{a}_{1} + y_{1} \, \mathbf{a}_{2} + z_{1} \, \mathbf{a}_{3} & = & y_{1}b \, \mathbf{\hat{y}} + z_{1}c \, \mathbf{\hat{z}} & \left(8f\right) & \text{Si I} \\ \mathbf{B}_{2} & = & y_{1} \, \mathbf{a}_{1}-y_{1} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{1}\right) \, \mathbf{a}_{3} & = & -y_{1}b \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{1}\right)c \, \mathbf{\hat{z}} & \left(8f\right) & \text{Si I} \\ \mathbf{B}_{3} & = & -y_{1} \, \mathbf{a}_{1} + y_{1} \, \mathbf{a}_{2} + \left(\frac{1}{2} - z_{1}\right) \, \mathbf{a}_{3} & = & y_{1}b \, \mathbf{\hat{y}} + \left(\frac{1}{2}-z_{1}\right)c \, \mathbf{\hat{z}} & \left(8f\right) & \text{Si I} \\ \mathbf{B}_{4} & = & y_{1} \, \mathbf{a}_{1}-y_{1} \, \mathbf{a}_{2}-z_{1} \, \mathbf{a}_{3} & = & -y_{1}b \, \mathbf{\hat{y}}-z_{1}c \, \mathbf{\hat{z}} & \left(8f\right) & \text{Si I} \\ \mathbf{B}_{5} & = & -y_{2} \, \mathbf{a}_{1} + y_{2} \, \mathbf{a}_{2} + z_{2} \, \mathbf{a}_{3} & = & y_{2}b \, \mathbf{\hat{y}} + z_{2}c \, \mathbf{\hat{z}} & \left(8f\right) & \text{Si II} \\ \mathbf{B}_{6} & = & y_{2} \, \mathbf{a}_{1}-y_{2} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{2}\right) \, \mathbf{a}_{3} & = & -y_{2}b \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{2}\right)c \, \mathbf{\hat{z}} & \left(8f\right) & \text{Si II} \\ \mathbf{B}_{7} & = & -y_{2} \, \mathbf{a}_{1} + y_{2} \, \mathbf{a}_{2} + \left(\frac{1}{2} - z_{2}\right) \, \mathbf{a}_{3} & = & y_{2}b \, \mathbf{\hat{y}} + \left(\frac{1}{2}-z_{2}\right)c \, \mathbf{\hat{z}} & \left(8f\right) & \text{Si II} \\ \mathbf{B}_{8} & = & y_{2} \, \mathbf{a}_{1}-y_{2} \, \mathbf{a}_{2}-z_{2} \, \mathbf{a}_{3} & = & -y_{2}b \, \mathbf{\hat{y}}-z_{2}c \, \mathbf{\hat{z}} & \left(8f\right) & \text{Si II} \\ \mathbf{B}_{9} & = & -y_{3} \, \mathbf{a}_{1} + y_{3} \, \mathbf{a}_{2} + z_{3} \, \mathbf{a}_{3} & = & y_{3}b \, \mathbf{\hat{y}} + z_{3}c \, \mathbf{\hat{z}} & \left(8f\right) & \text{Si III} \\ \mathbf{B}_{10} & = & y_{3} \, \mathbf{a}_{1}-y_{3} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{3}\right) \, \mathbf{a}_{3} & = & -y_{3}b \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{3}\right)c \, \mathbf{\hat{z}} & \left(8f\right) & \text{Si III} \\ \mathbf{B}_{11} & = & -y_{3} \, \mathbf{a}_{1} + y_{3} \, \mathbf{a}_{2} + \left(\frac{1}{2} - z_{3}\right) \, \mathbf{a}_{3} & = & y_{3}b \, \mathbf{\hat{y}} + \left(\frac{1}{2}-z_{3}\right)c \, \mathbf{\hat{z}} & \left(8f\right) & \text{Si III} \\ \mathbf{B}_{12} & = & y_{3} \, \mathbf{a}_{1}-y_{3} \, \mathbf{a}_{2}-z_{3} \, \mathbf{a}_{3} & = & -y_{3}b \, \mathbf{\hat{y}}-z_{3}c \, \mathbf{\hat{z}} & \left(8f\right) & \text{Si III} \\ \end{array} \]References
- D. Y. Kim, S. Stefanoski, O. O. Kurakevych, and T. A. Strobel, Synthesis of an open–framework allotrope of silicon, Nat. Mater. 14, 169–173 (2015), doi:10.1038/NMAT4140.