The Monoclinic Crystal System
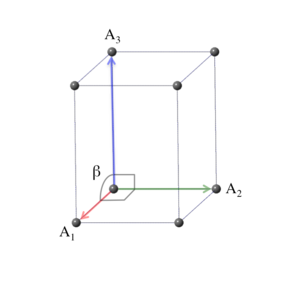
In the monoclinic crystal system, the conventional unit cell
is defined by primitive vectors of arbitrary length, where one of the
vectors is perpendicular to the other two. Modern convention chooses
this vector to be the one with length $b$ (or unique axis $b$
in the literature), so that $\alpha = \gamma = \pi/2$ and $\beta \ne
\pi/2$. Note that this orientation differs from that
of Setyawan
and Curtarolo, who used a unique axis $a$
setting. Their
angle $\alpha$ would be $\beta$ in our notation. The conventional unit
cell can be described by the vectors
\[ \begin{array}{ccc} \mathbf{A}_1 & = & a \, \mathbf{\hat{x}} \nonumber \\ \mathbf{A}_2 & = & b \, \mathbf{\hat{y}} \nonumber \\ \mathbf{A}_3 & = & c \, \cos\beta \, \mathbf{\hat{x}} + c \, \sin\beta \, \mathbf{\hat{z}}, \end{array} \]
and the volume of a conventional unit cell is \[ V = a \, b \, c \, \sin\beta. \]
Lattice 2: Simple Monoclinic
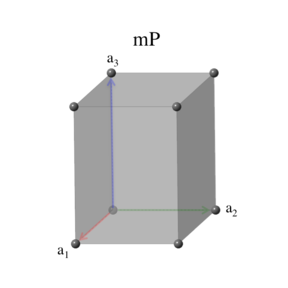
The simple monoclinic cell is identical to the conventional cell:
\[ \begin{array}{ccc} \mathbf{a}_1 & = & a \, \mathbf{\hat{x}} \nonumber \\ \mathbf{a}_2 & = & b \, \mathbf{\hat{y}} \nonumber \\ \mathbf{a}_3 & = & c \, \cos\beta \, \mathbf{\hat{x}} + c \, \sin\beta \, \mathbf{\hat{z}}, \end{array} \]
and the cell volume is just \[ V = a \, b \, c \, \sin\beta. \]
The space groups associated with the simple monoclinic lattice are:
\[ \begin{array}{lll} 3. ~ \text{P2} & 4. ~ \text{P2$_{1}$} & 6. ~ \text{Pm} \\ 7. ~ \text{Pc} & 10. ~ \text{P2/m} & 11. ~ \text{P2$_{1}$/m} \\ 13. ~ \text{P2/c} & 14. ~ \text{P2$_{1}$/c} & \\ \end{array} \]
Lattice 3: Base-Centered Monoclinic
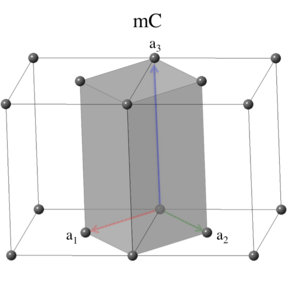
The base-centered monoclinic lattice is in the same crystal system as the monoclinic lattice, but its periodicity allows an additional translation in the plane defined by $\mathbf{a}_1$ and $\mathbf{a}_2$. The primitive vectors for the base-centered monoclinic lattice can be written as
\[ \begin{array}{ccc} \mathbf{a}_1 & = & \frac{a}{2} \, \mathbf{\hat{x}} - \frac{b}{2} \, \mathbf{\hat{y}} \nonumber \\ \mathbf{a}_2 & = & \frac{a}{2} \, \mathbf{\hat{x}} + \frac{b}{2} \, \mathbf{\hat{y}} \nonumber \\ \mathbf{a}_3 & = & c \, \cos\beta \, \mathbf{\hat{x}} + c \, \sin\beta \, \mathbf{\hat{z}}. \end{array} \]
The volume of the base-centered monoclinic unit cell is \[ V = \left(\frac{1}{2}\right) \, a \, b \, c \, \sin\beta, \] which is half that of the conventional unit cell.
The space groups associated with the base-centered monoclinic lattice are
\[ \begin{array}{lll} 5. ~ \text{C2} & 8. ~ \text{Cm} & 9. ~ \text{Cc} \\ 12. ~ \text{C2/m} & 15. ~ \text{C2/c} & \\ \end{array} \]
The labels for these space groups all begin with $\text{C}$,
indicating the base-centered translation associated with
these groups. The International Tables offer two
representations of the base-centered monoclinic space
groups, one for unique axis $b$
and one for unique
axis $c$
, where $\alpha \ne \pi/2$ and $\beta =
\pi/2$. Space group 5 is then listed as B2
or C2
depending on this choice. Most authors ignore
this distinction, as will we.