Two Dimensional Periodic Systems: Part III

Possible Two Dimensonal Lattices

In the previous article we discussed the general problem of lattices and translational symmetry in two dimensions. We did not consider other symmetries possible in two dimensions: rotations, mirroring, and inversions.

Here we'll discuss the possible lattices that can be drawn in two dimensions. We'll see that they are limited by the requirements of translational and rotational symmetry. The next article will put it all together and look at the full set of symmetries available in two dimensions, and list all of the Wyckoff positions for each of the seventeen plane groups.

Let's start by dividing the possible lattices by their rotational symmetry. That is, we'll rotate the lattice around its origin and see how far we can get before we recover the original lattice. In general that will be some value 360°/$n$, where $n$ is an integer. Obviously this implies that rotations $m$ × 360°/$n$ also reproduce the lattice, so we say such a lattice has n-fold rotation symmetry, or a holohedry of $n$.^† All lattices with the same holohedry from a Crystal System. Given that, we'll list the lattices in increasing order of $n$.

Parallelogram Crystal System (Holohedry 1)

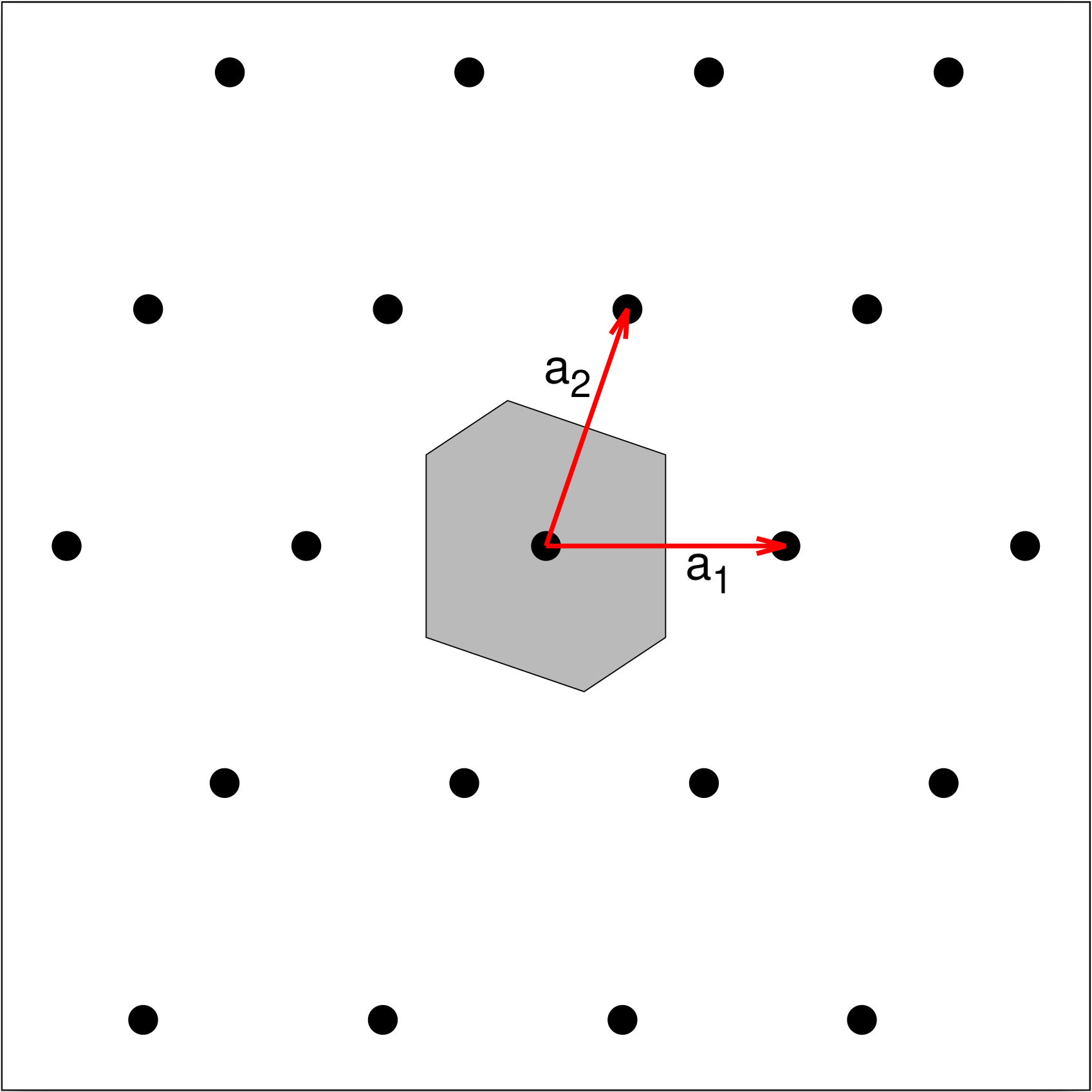
Figure 1: The general “parallelogram” lattice generated by the primitive vectors (1). The Wigner-Seitz cell for the system is shaded in gray.

The Parallelogram

The most general lattice in two dimensions, called rather unimaginatively the parallelogram, is shown in Fig. 1. We've chosen to align the lattice in a standard orientation, with the primitive vector $\mathbf{a}_{1}$ aligned along the x-axis:

$\begin{array}{ccccr} \mathbf{a}_{1} & = & a \, \hat{x} & \\ \mathbf{a}_{2} & = & b \cos\gamma \, \hat{x} + b \sin\gamma \, \hat{y} & , \end{array}$ (1) where γ is the angle between the two vectors. This is a convention, as $\mathbf{a}_{1}$ can point in any direction, and the only real requirement to define the lattice is that we know a, b and &gamma:. The area of the lattice is $A = a \, b \, \sin\gamma$ , (2) and in this standard representation the reciprocal lattice vectors are $\begin{array}{ccccr} \mathbf{b}_{1} & = & 2 \pi \left(\sin\gamma \, \hat{x} - \cos\gamma \, \hat{y} \right)/(a \sin\gamma) \\ \mathbf{b}_{2} & = & 2 \pi/(b \cos\gamma) \, \hat{y} & . \end{array}$ (3)

Every lattice in two dimensions can be placed in the form (1), but we will reserve this name for a lattice that does not have a higher rotational symmetry. This means that we'll call a lattice a parallelogram if and only if:

$ \gamma \ne \pm 60^\circ ~ , ~ \pm 90^\circ$ or $\pm 120^\circ$ , (4) and $a \ne b$ . (5) This requirement might seem to come from out of the blue, but it will become clear when we look at the centered rectangular lattice.

Certain linear combinations of primitive vectors can also move the lattice to a higher symmetry, e.g.,

$\mathbf{a}_1 \cdot (\mathbf{a}_{2} - \mathbf{a}_{1}) = 0$ , (6) which implies that we can find a set of primitive vectors where γ = 90°.

Fig. 1 also shows the Wigner-Seitz cell for the lattice. The rather distorted hexagon is a characteristic of the general parallelogram lattice.

Rectangular Crystal System (Holohedry 2)

There are two lattices which have 2-fold rotation symmetry, the rectangular lattice and the “centered” rectangular lattice.

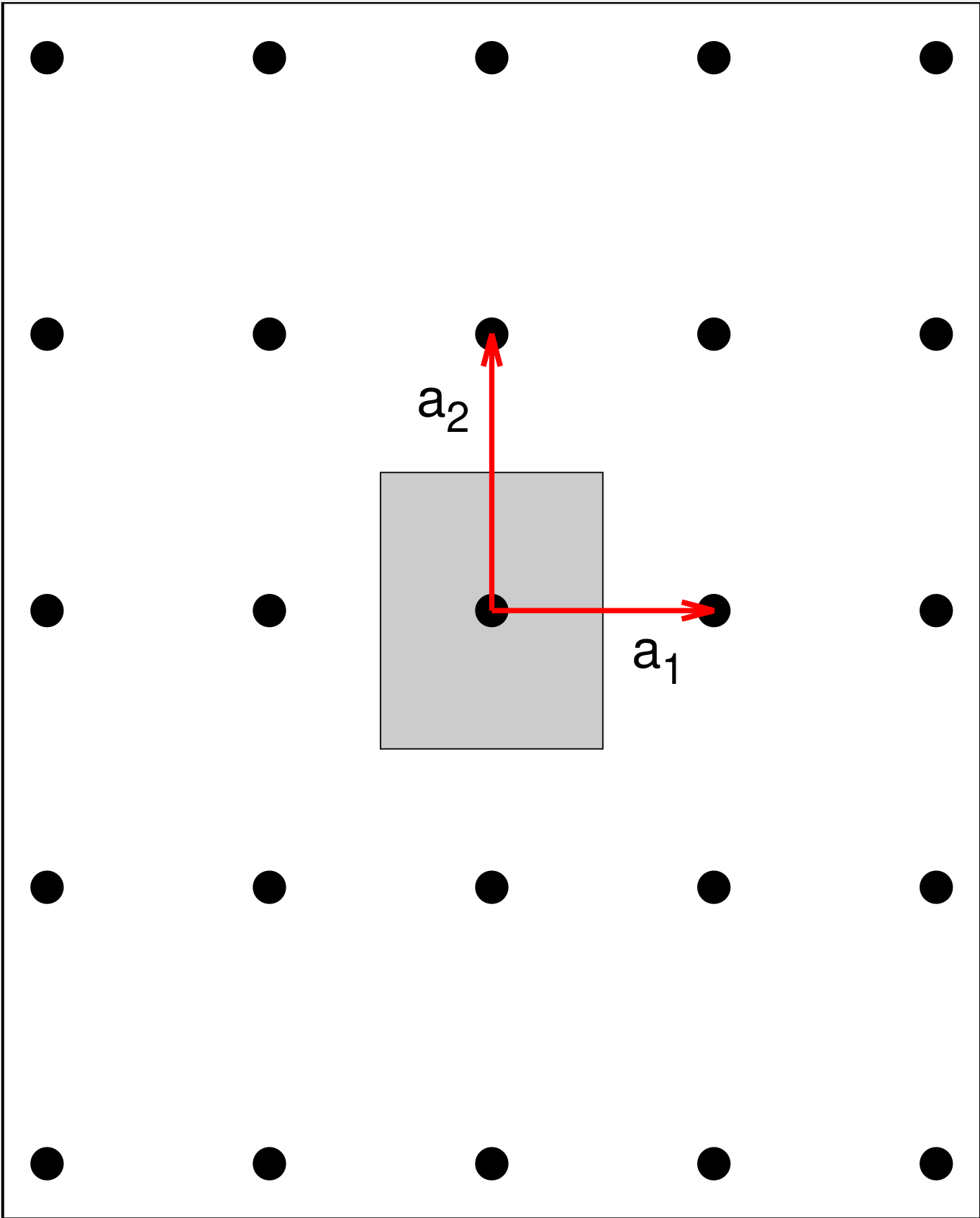
Figure 2: A rectangular lattice generated by the primitive vectors (8). The general condition is that γ = 90° and $a \ne b$. The Wigner-Seitz cell for the system, which is also a rectangle, is shaded in gray.

The Rectangular Lattice

A simple rectangular lattice is shown in Fig. 2, along with its Wigner-Seitz cell. As you might guess, the lattice is defined by the conditions

$\mathbf{a}_{1} \cdot \mathbf{a}_{2} = 0$ and $a \ne b$ . (7) The first condition implies γ = 90° (1). Violation of the second condition would give a square lattice, which we'll discuss when we get to 4-fold rotations.

In our standard orientation, the primitive vectors of this lattice are

$\begin{array}{ccc} \mathbf{a}_{1} & = & a \, \hat{x} ~ , \\ \mathbf{a}_{2} & = & b \, \hat{y} ~ , \end{array}$ (8) the area of the lattice is $A = a \, b$ , (9) and the reciprocal lattice vectors are rather boringly $\begin{array}{ccc} \mathbf{b}_{1} & = & \frac{2\pi}{a} \, \hat{x} ~ , \\ \mathbf{b}_{2} & = & \frac{2\pi}{b} \, \hat{y} ~ . \end{array}$ (10)

The Centered Rectangular Lattice

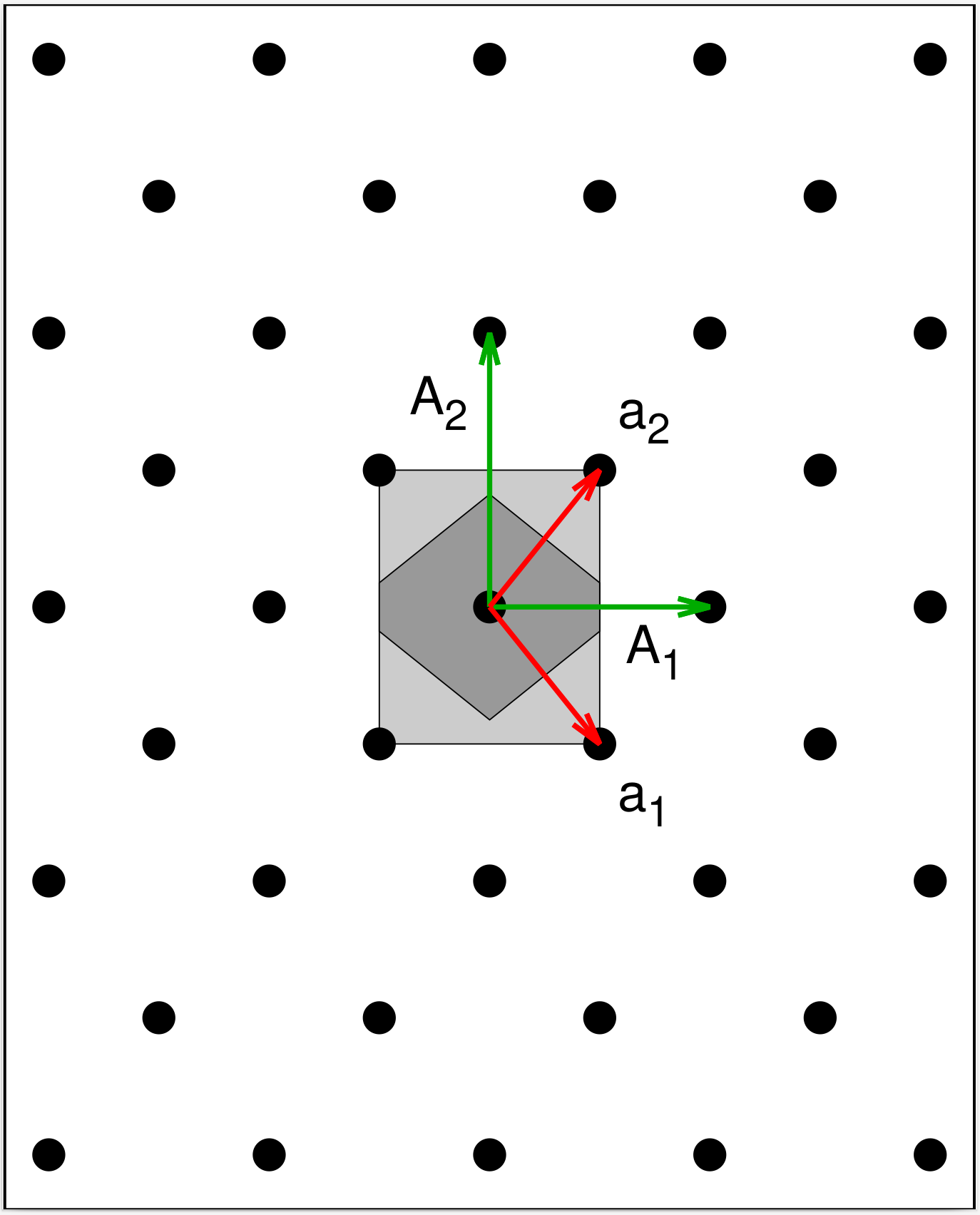
Figure 3: A centered rectangular lattice generated by the primitive vectors (11). The red vectors are the actual primitive vectors of the lattice, with its Wigner-Seitz cell shaded in dark gray. The green vectors form the rectangular *conventional lattice* (16), with its corresponding Wigner-Seitz cell, twice as large as the primitive cell, shaded in lighter gray. Since the conventional cell is twice as large as the primitive cell it contains two primitive lattice points.

Now consider the lattice in Fig. 3. It it is identical to the one in Fig. 2 except for the spots added in the middle of each rectangle. As such, this is a rectangular system with additional translational symmetry. The primitive vectors of the lattice (in our standard notation) are

$\begin{array}{ccc} \mathbf{a}_{1} & = & \frac12 a \, \hat{x} - \frac12 b \, \hat{y} ~ \\ \mathbf{a}_{2} & = & \frac12 a \, \hat{x} + \frac12 b \, \hat{y} ~ , \end{array}$ (11) the reciprocal vectors are $\begin{array}{ccc} \mathbf{b}_{1} & = & \frac{2\pi}{a} \, \hat{x} - \frac{2\pi}{b} \, \hat{y} \\ \mathbf{b}_{2} & = & \frac{2\pi}{a} \, \hat{x} + \frac{2\pi}{b} \, \hat{y} ~ , \end{array}$ (12) and the area of the cell is $A = \frac12 \, a \, b$ . (13)

Just as with the parallelogram there are special cases when this system is kicked up to a higher rotational symmetry. These are

$a = b$ , (14) when the lattice becomes square (4-fold rotation), and $b = \frac{1}{\sqrt3} \, a$ or $\sqrt{3} \, a$ , (15) when the lattice becomes hexagonal (3-fold or 6-fold rotation).

Although (11) is the most compact way of defining the lattice, it is often useful to explicitly refer to its underlying rectangular nature. To this end we define the conventional lattice, with “primitive” vectors

$\begin{array}{ccc} \mathbf{A}_{1} = & \mathbf{a}_{1} + \mathbf{a}_{2} & = a \, \hat{x} \\ \mathbf{A}_{2} = & \mathbf{a}_{2} - \mathbf{a}_{1} & = b \, \hat{y} ~ . \end{array}$ (16) These are the green arrows in Fig. 3, and are in exactly the same form as the standard rectangular lattice (8), which means that the area of the conventional cell is just $a b$, twice as large as the primitive cell.

Crystallographers ordinarily give positions in terms of the conventional lattice rather than the primitive lattice. This seems confusing until we realize that (11) is not a unique way to define the primitive centered lattice. We could just as easily have picked

$\begin{array}{ccc} \mathbf{a}_{1} & = & a \, \hat{x} \\ \mathbf{a}_{2} & = & \frac12 a \, \hat{x} + \frac12 b \, \hat{y} ~ . \end{array}$ (17) This set of primitive vectors gives exactly the same lattice as (8), but the lattice coordinates would be different in each case. Thus crystallographers ordinarily designate the lattice of this point as $(x,y)$. To emphasize that this is a point in a centered lattice, it is often written as $(x,y); (0,0)+ ~ (1/2,1/2)+$ to remind us that there are two equivalent points in the conventional cell.

Trigonal Crystal System (Holohedry 3)

As we will see below, a lattice with 3-fold rotational symmetry will also have 6-fold rotational symmetry, so we will postpone this discussion until we get to $n = 6$.

Square Crystal System (Holohedry 4)

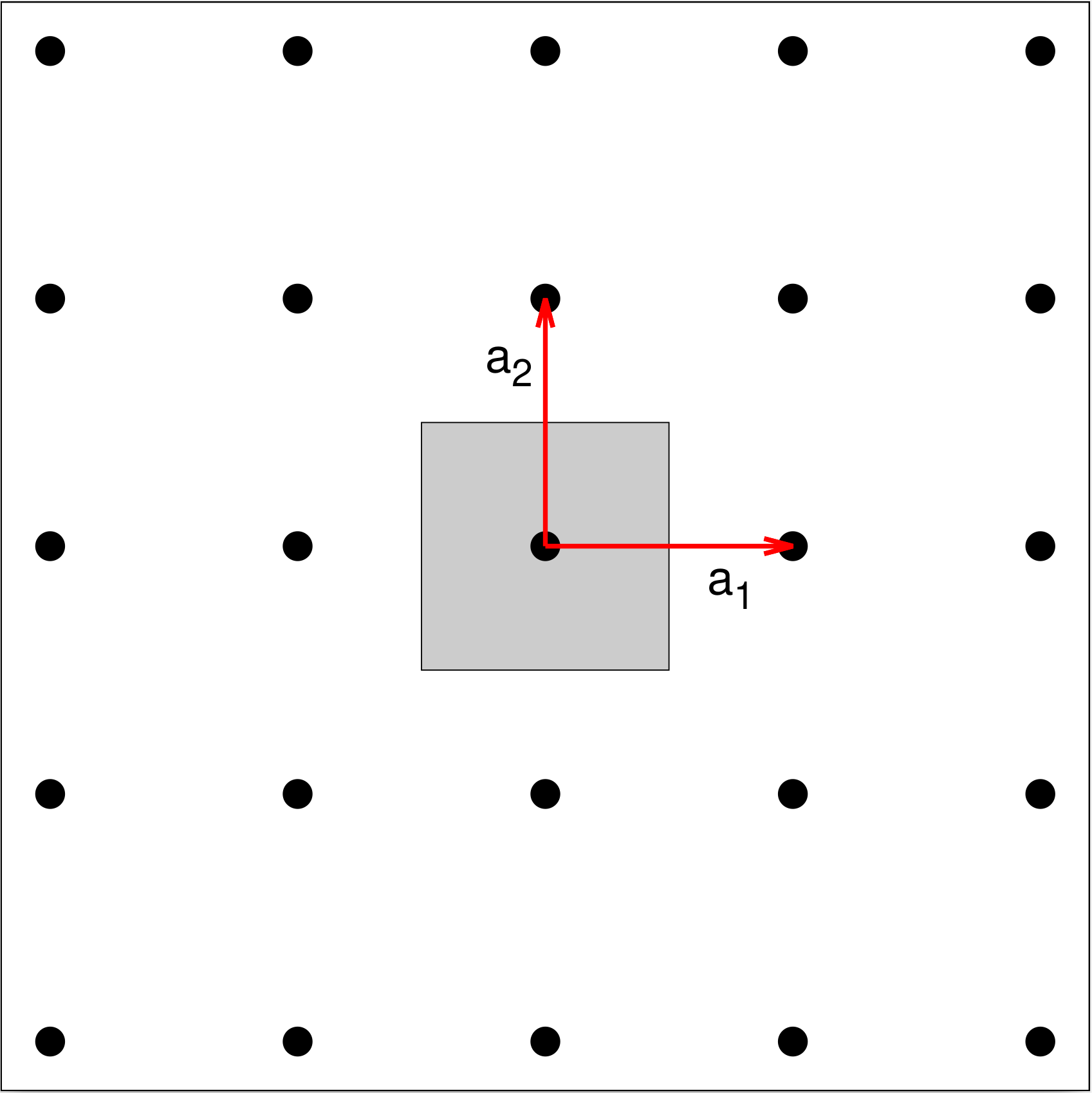
The Square Lattice

This is perhaps the simplest lattice: the primitive vectors are orthogonal to one another and equal in length:

$\begin{array}{ccc} \mathbf{a}_{1} & = & a \, \, \hat{x} \\ \mathbf{a}_{2} & = & a \, \hat{y} ~ , \end{array}$ (19) the reciprocal lattice has the same properties: $\begin{array}{ccc} \mathbf{b}_{1} & = & \frac{2\pi}{a} \, \hat{x} ~ \\ \mathbf{b}_{2} & = & \frac{2\pi}{a} \, \hat{y} ~ , \end{array}$ (20) and the area of the primitive cell is $A = a^2$ . (21) The lattice and its corresponding (square) Wigner-Seitz cell are shown in Fig. 4.

5-fold Rotational Symmetry (Holohedry 5)

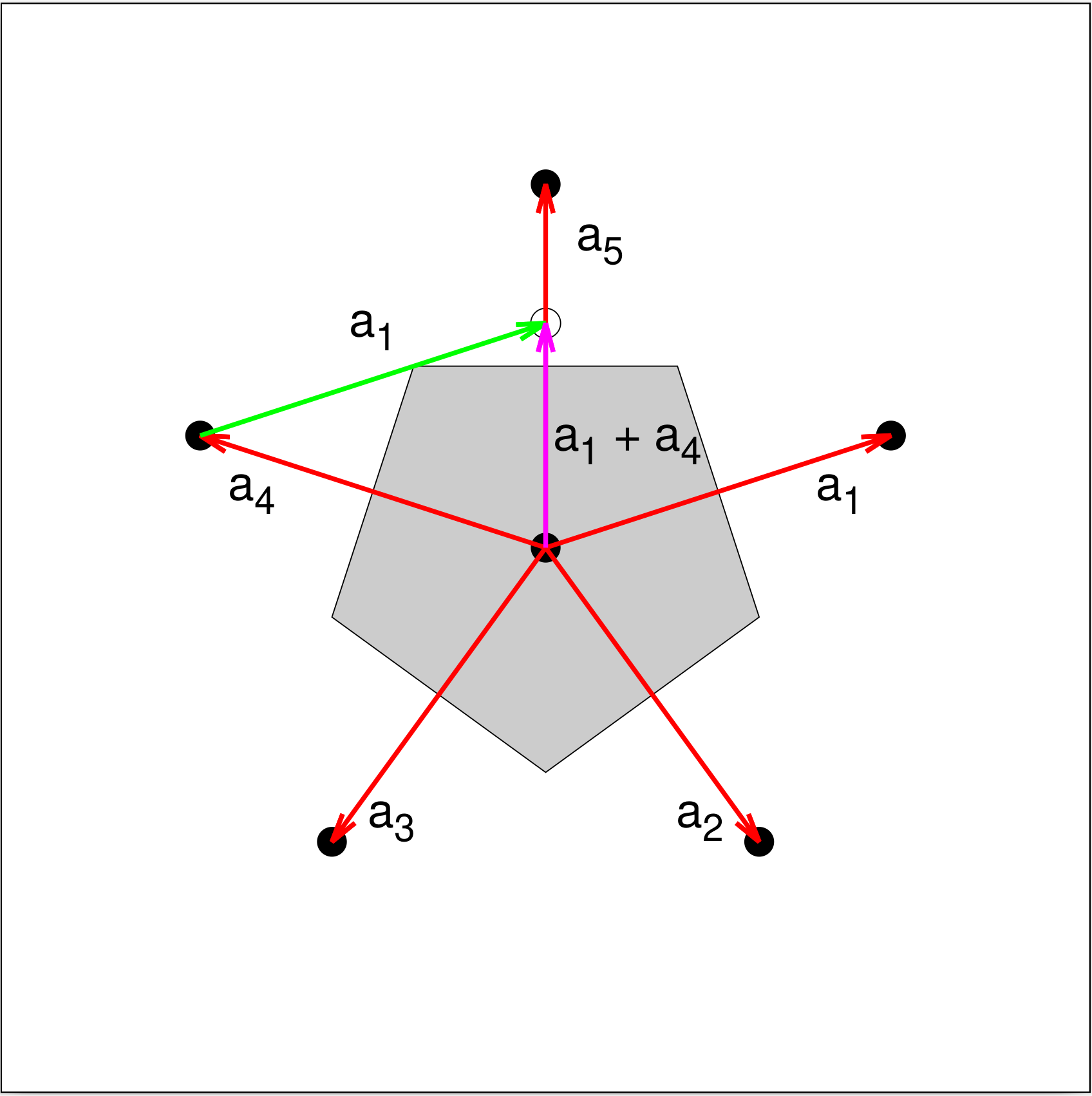
Figure 5: Possible primitive vectors for a cell with five-fold rotational symmetry, and the hypothetical Wigner-Seitz cell, shaded in gray. If we take $\mathbf{a}_{1}$ and $\mathbf{a}_{4}$ as the primitive vectors of the lattice, then translational symmetry demands that there be a lattice point at $\mathbf{a}_{1} + \mathbf{a}_{4}$. This breaks the pentagonal symmetry, and so there are no lattices with a five-fold rotation axis in two (or three) dimensions. Adapted from “The symmetry of crystals. The crystallographic restriction theorem.”²

While quasicrystals³ show five-fold rotational symmetry, they are not true crystals, as they do not have translational symmetry. This can be seen in \reffig{fig:pentagon}. Here we show six points in a hypothetical lattice with a 5-fold rotation axis. The vectors $\mathbf{a}_{1}$ through $\mathbf{a}_{5}$ are candidate lattice vectors. If we arbitrarily pick $\mathbf{a}_{1}$ and $\mathbf{a}_{4}$ as our primitive vectors, then we should be able to write all of the $\mathbf{a}_{i}$ in the form

$\mathbf{a}_{i} = n_{1} \mathbf{a}_{1} + n_{4} \mathbf{a}_{4}$ (22) for integer $n_{i}$. In the figure we show that this is not the case for $\mathbf{a}_{1} + \mathbf{a}_{4}$, and so five-fold rotations are forbidden.

This is a specific case of the Crystallographic restriction theorem, which states that two- and three-dimensional lattices can only have 1-, 2-, 3-, 4- and 6-fold rotation axis. Bamberg et al.⁴ prove the theorem for all dimensions, but Wikipedia⁵ has a much more understandable proof for two and three dimensions.

Hexagonal Crystal System (Holohedry 6)

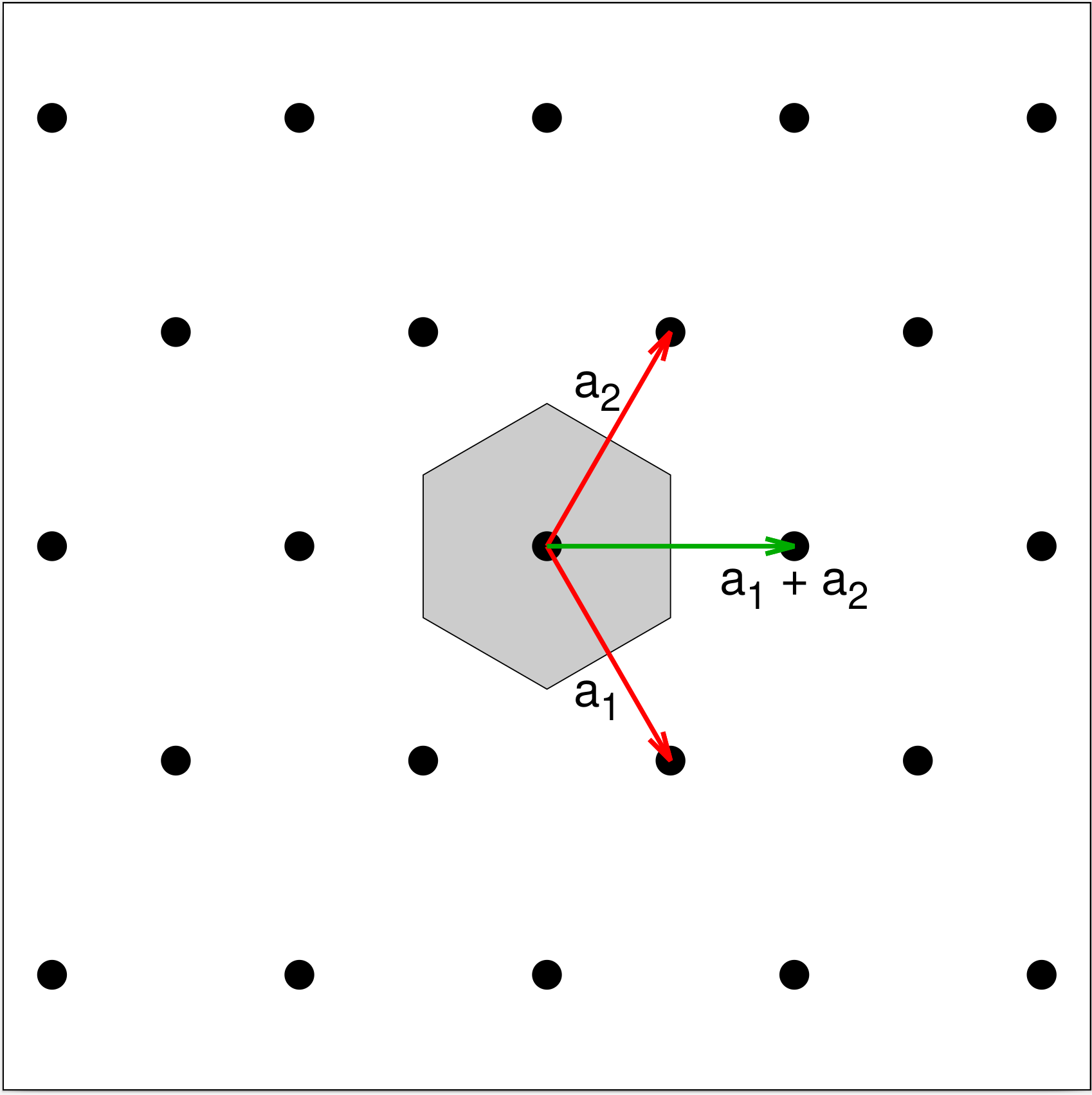
The Hexagonal Lattice

If we set $b = \sqrt{3} a$ in the centered rectangular lattice (11) we find the primitive vectors

$\begin{array}{ccc} \mathbf{a}_{1} & = & \frac12 a \, \hat{x} - \frac{\sqrt{3}}{2} a \, \hat{y} ~ \\ \mathbf{a}_{2} & = & \frac12 a \, \hat{x} + \frac{\sqrt{3}}{2} a \, \hat{y} ~ . \end{array}$ (23) When we do this the resulting lattice has a six-fold rotation axis, as shown in Fig. 6. This also implies that the lattice has a three-fold rotation axis, as mentioned above. We can therefore use this lattice for systems with trigonal as well as hexagonal symmetry.

The reciprocal lattice vectors associated with (23) are

$\begin{array}{ccc} \mathbf{b}_{1} & = & \frac{2\pi}{a} \left(\hat{x} - \frac{1}{\sqrt{3}} \, \hat{y} \right) ~ \\ \mathbf{b}_{2} & = & \frac{2\pi}{a} \left(\hat{x} + \frac{1}{\sqrt{3}} \, \hat{y} \right) ~ , \end{array}$ (24) and the area of the primitive cell is $A = \frac{\sqrt{3}}{2} a^2$ . (25)

Since the hexagonal lattice is an offshoot of the centered rectangular lattice, you might think that lattice coordinates would be given in terms of the corresponding “conventional” unit cell as in (16) with $b = \sqrt{3}a$. This turns out not to be the case. Lattice coordinates $(x,y)$ are always given in terms of the vectors (23):

$\begin{array}{ccc} \mathbf{B} & = & x \, \mathbf{a}_{1} + y \, \mathbf{a}_{2} \\ & = & \frac12 a (x + y) \, \hat{x} + \frac{\sqrt{3}}{2} a (y - x) \, \hat{y} ~ . \end{array}$ (26) This leads to rather interesting notation when we apply a 60° or 120° rotation. For example, suppose our lattice has a 3-fold rotation axis. Then if there is an atom at the point (26), then there will be another point at $\begin{array}{ccc} \mathbf{B} & = & x \mathbf{a}_{2} - y (\mathbf{a}_{1} + \mathbf{a}_{2}) \\ & = & \frac12 a (x - 2 y) \, \hat{x} + \frac{\sqrt{3}}{2} a x \, \hat{y} \\ & = & -y \, \mathbf{a}_{1} + (x-y) \, \hat{a}_{2} ~ , \end{array}$ (27) and another at $\begin{array}{ccc} \mathbf{B} & = & - x (\mathbf{a}_{1} + \mathbf{a}_{2}) + y \mathbf{a}_{1} \\ & = & \frac12 a (y - 2 x) \, \hat{x} - \frac{\sqrt{3}}{2} a y \, \hat{y} \\ & = & (y - x) \, \mathbf{a}_{1} - x \, \mathbf{a}_{2} ~ . \end{array}$ (28) As we'll see in the next article, tables listing Wyckoff positions for a three-fold rotation will list a general three-fold rotation by the hexagonal coordinates $(x,y)$ , $(-y,x-y)$ and $(y-x,x)$ . (29)

This concludes our enumeration of the possible two dimensional lattices. Next we'll decorate those lattices with “atoms” and see what kinds of symmetries are available to us.

Glossary

Here is a brief definition of some of the terms used in this article:

Crystal Class: The set of all lattices which have the same holohedry.
Crystallographic Restriction Theorem: Theorem^{2, 4,
5} which states that a two- or three-dimensional lattice can only have a 1-, 2-, 3-, 4-, or 6-fold rotation axis. In particular, 5-fold lattices, which would have a pentagonal Wigner-Seitz cell, are forbidden.
Holohedry: The point group of a lattice which describes its rotational symmetry, without translations, mirrors, glides, or inversion. In two dimensions the only possibilities are 1-, 2-, 3-, 4-, and 6-fold rotations (rotations by 360°, 180°, 120°, 90°, and 60°, respectively) about the origin.
n-fold Rotation Axis: A rotation of the crystal by 360°/n which replicates the original crystal. The only allowed values of n are 1, 2, 3, 4, and 6.
Plane Group: A group which lists possible symmetry elements that leave a two-dimensional crystal unchanged. There are seventeen plane groups. The three dimension analog of the plane groups are the 230 space groups.
Quasicrystal: A solid which exhibits a 5-fold (icosahedral) rotational symmetry.³ It is not a crystal, as it does not exhibit translational symmetry or long-range order. See the Crystallographic Restriction Theorem.
Standard Orientation: The preferred orientation of the primitive vectors in a lattice. This is purely a matter of convention. You are allowed replace the “standard” primitive vectors with any linear combinations of the primitive vectors which do not change the area of the unit cell. We will in general follow the {\AFLOW} standard convention.⁸
Wigner-Seitz Cell: A uniquely defined unit cell consisting of all spatial points closer to a given lattice point than to any other lattice point.
Wyckoff Positions: Subsets of a given plane or space group.

References

M. Lax, Symmetry Principles in Solid State and Molecular Physics (J. Wiley & Sons, New York, 1974), chap. 6, pp. 169–175. Avaliable from the Internet Archive at https://archive.org/details/symmetryprincipl0000laxm
The symmetry of crystals. The crystallographic restriction theorem. https://www.xtal.iqfr.csic.es/Cristalografia/parte_03_1_1-en.html.
W. Steurer, Quasicrystals: What do we know? What do we want to know? What can we know?, Acta Crystallographica A 74, 1–11 (2018), doi:10.1107/S2053273317016540.
J. Bamberg, G. Cairns, and D. Kilminster, The Crystallographic Restriction, Permutations, and Goldbach’s Conjecture, American Mathematical Monthly 110, 202–209 (2003), doi:10.1080/00029890.2003.11919956.
Crystallographic restriction theorem – Dimensions 2 and 3. https://en.wikipedia.org/wiki/Crystallographic_restriction_theorem#Dimensions_2_and_3.
D. Hicks, M. J. Mehl, E. Gossett, C. Toher, O. Levy, R. M. Hanson, G. L. W. Hart, and S. Curtarolo, The AFLOW Library of Crystallographic Prototypes: Part 2, Comput. Mater. Sci. 161, S1–S1011 (2019), doi:10.1016/j.commatsci.2018.10.043.
B. Souvignier, Group theory applied to crystallography (International Union of Crystallography, Radboud University Nijmegen, The Netherlands, 2008). https://www.math.ru.nl/~souvi/krist_09/cryst.pdf
W. Setyawan and S. Curtarolo, High-throughput electronic band structure calculations: Challenges and tools, Comput. Mater. Sci. 49, 299–312 (2010), doi:10.1016/j.commatsci.2010.05.010.

Footnotes

^†It is not really proper to designate the holohedry of the system by its rotations,¹ but it is sufficient in two dimensions. We'll address the three dimensional case in another article.

Encyclopedia of Crystallographic Prototypes